三选一：见风使舵

问题是一个朋友提起的：如果有三扇门，一扇门里是法拉利，其他两扇是山羊。请你选一扇门。选到什么里面的东西就归你。

当你选完之后，我打开没被你选过的两扇门中的一扇，里面是山羊。现在还剩两扇门，你换不换选项？

可能这个问题你很早就听说过了，但我还是要公布一下答案，此时你换选项得到法拉利的概率是坚持原来选择的两倍。一开始我对这个结果十分吃惊，这完全是随机的举动怎么可能有那么大的差别。我甚至列了一个表格说明剩下两个选择的概率各为50%。

朋友向我解释，原本三个选项abc的概率各为1/3，你选了a，也就是a的概率为1/3，b、c的概率为2/3。可是排除b、c其中一个之后，另一个的概率就独占了2/3，a还是保持1/3不变。

另外一个解释方法是：现在假设有两个人，甲和乙，甲永远坚持自己第一次猜测，乙永远在打开一扇门后改变自己的想法。不难发现的是，只要乙第一次没猜对，那么第二次一定能够猜对; 如果乙第一次就猜对了，那第二次一定猜错。然而最后的结果只看第二次，所以猜对的可能性就是第一次猜错的可能性：2/3，猜错的可能性成了第一次猜对的可能性：1/3。

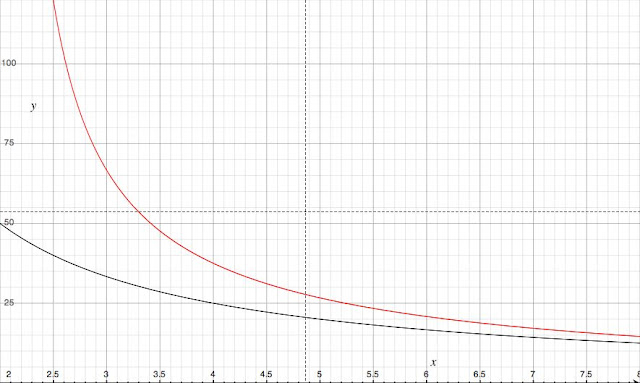
所以，引伸一下，如果是一道n选一的题目，以这种模式进行。坚持的概率：1/n；见风使舵的概率：(n-1)/(n(n-2))。看下面这幅图：

x轴是选择的数量，y轴是百分比。红线是见风使舵，黑线是坚持到底。

负责声明：以上讨论仅限理论研究，请勿擅自应用于考试中。请勿跨省追捕。